深入浅出了解生成模型-4：一致性模型（consistency model）

前面已经介绍了扩散模型，在最后的结论里面提到一点：扩散模型往往需要多步才能生成较为满意的图像。不过现在有一种新的方式来加速（旨在通过少数迭代步骤）生成图像：一致性模型（consistency model），因此这里主要是介绍一致性模型（consistency model）基本原理以及代码实践，值得注意的是本文不会过多解释数学原理，数学原理推导可以参考：

介绍一致性模型之前需要了解几个知识：在传统的扩散模型中无论是加噪还是解噪过程都是随机的，在论文¹中（也就是CM作者宋博士的另外一篇论文）将这个随机过程（也就是随机微分方程SDE）转化成“固定的”过程（也就是常微分方程ODE），只有过程可控才能保证下面公式成立。

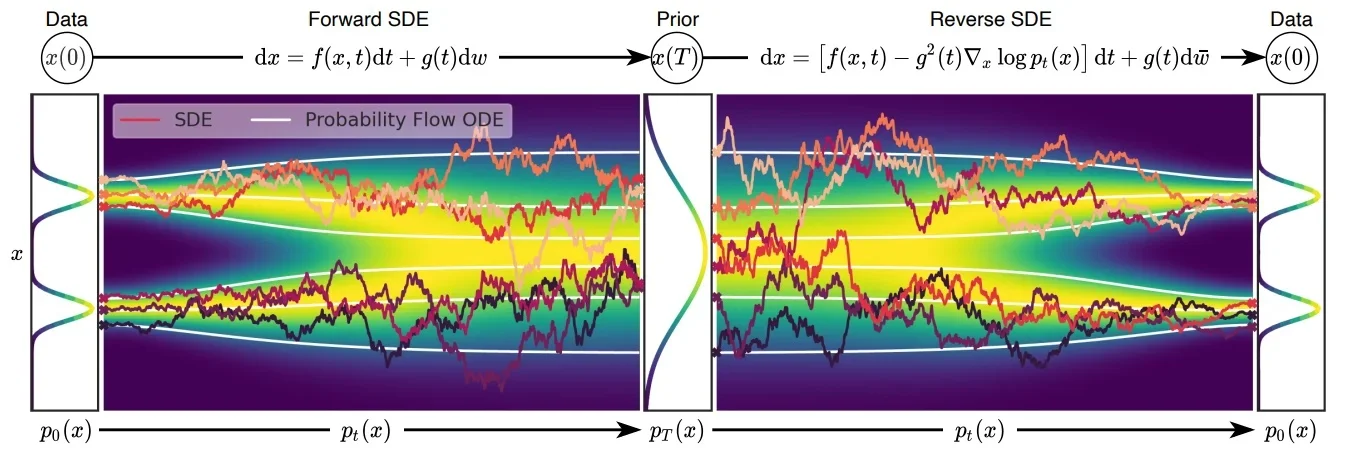
一致性模型（Consistency Model）

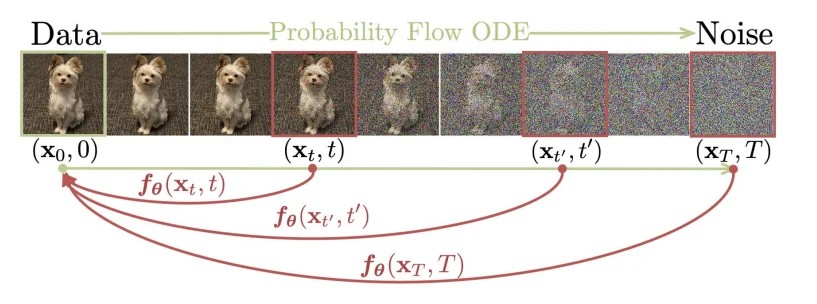
其中ODE（常微分方程），在传统的扩散模型（Diffusion Models, DM）中，前向过程是从原始图像 $x_0$开始，不断添加噪声，经过 $T$步得到高斯噪声图像 $x_T$。反向过程（如 DDPM）通常通过训练一个逐步去噪的模型，将 $x_T$逐步还原为 $x_0$ ，每一步估计一个中间状态，因此推理成本高（需迭代 T 步）。而在 Consistency Models（CM） 中，模型训练时引入了 Consistency Regularization，使得模型在不同的时间步 $t$都能一致地预测干净图像。这样在推理时，无需迭代多步，而是可以通过一个单一函数$f(x ,t)$ 直接将任意噪声图像$x_t$ 还原为目标图像$x_0$ 。这大大减少了推理时间，实现了一步（或少数几步）生成。

一致性模型（consistency model）在论文²里面主要是通过使用常微分方程角度出发进行解释的。Consistency Model 在 Diffusion Model 的基础上，新增了一个约束：从某个样本到某个噪声的加噪轨迹上的每一个点，都可以经过一个函数 $f$ 映射为这条轨迹的起点（也就是通过扩散处理的图像在不同的时间 $t$都可以直接转化为最开始的图像 $x_0$），用数学描述就是：$f:(x_t, t)\rightarrow x_\epsilon$，换言之就是需要满足： $f(x_t,t)=f(x_{t^\prime},t^\prime)$ 其中 $t,t^\prime \in [\epsilon,T]$，正如论文里面的图片描述：

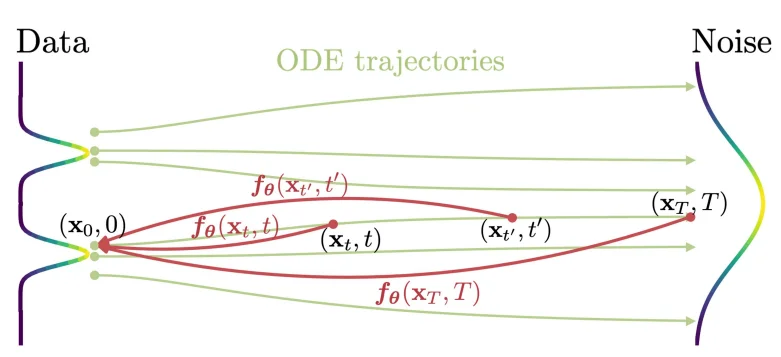
要满足上面的计算关系，作者在论文里面定义如下的等式关系：

\[f_\theta(x,t)=c_{skip}(t)x+ c_{out}(t)F_\theta(x,t)\]

其中等式需要满足：$c_{skip}(\epsilon)=1,c_{out}(\epsilon)=0$ （$c_{skip}(t)=\frac{\sigma_{data}^2}{(t- \epsilon)^2+ \sigma_{data}^2}$， $c_{out}(t)=\frac{\sigma_{data}(t-\epsilon)}{\sqrt{\sigma_{data}^2+ t^2}}$），随着解噪过程（时间从：$T \rightarrow \epsilon$ 其中 $c_{skip}$ 的值逐渐增大，也就是当前的解噪图像占比权重增加），其中我的 $F_\theta$ 就是我们的神经网络模型（比如Unet）。既然使用了神经网络那么必定就需要设计一个损失函数，在论文里面作者设计的损失函数为：两个时间步之间生成得到的图像距离通过最小化这个值（比如说 $\Vert x_{t+1} - x_t \Vert_2$）来优化模型参数。作者对于模型训练给出两种训练方式

直接通过蒸馏模型进行优化

通过直接蒸馏的方式对模型参数进行优化，其中设计的损失函数为：

\[\mathcal{L}_{CD}^N(\boldsymbol{\theta},\boldsymbol{\theta}^-;\phi) = \mathbb{E}[\lambda(t_n)d(\boldsymbol{f}_{\boldsymbol{\theta}}(\mathbf{x}_{t_{n+1}},t_{n+1}),\boldsymbol{f}_{\boldsymbol{\theta}^-}(\hat{\mathbf{x}}_{t_n}^{\boldsymbol{\phi}},t_n))]\]

其中 $d$代表距离（比如$l_1$或者 $l_2$）对于上面公式中几个参数：$\theta, \theta^-$，其中 $\hat{x}_{t_n}^\phi$ 代表的是一个预训练的 score model。虽然在CM中损失函数设计上一下子又3个模型，但是实际训练过程中更新的只有一个参数：$\theta$。另外一个参数是直接通过：$\theta^- \leftarrow \mu \theta^-+ (1-\mu \theta) $ 通过指数滑动平均方式进行训练。而另外一个参数 $\phi$是一个确定的函数直接通过ODE solver来进行计算得到，比如在论文³的使用的欧拉求解法：

\[\hat{x}_{t_n}^\phi= x_{t_{n+1}}- (t_n- t_{n+1})t_{n+1}\nabla_{x_{t_{n+1}}}\log p_{t_{n+1}}(x_{t_{n+1}})\]

欧拉法： $y_{n+1}= y_n+h*f(t_n, y_n)$ 其中h代表时间步长，f代表当前导数估计。不过值得进一步了解的是，在DL中大部分函数都是直接通过神经网络进行“估算的”，也就是说对于上面的 $\nabla_{x_{t_{n+1}}}\log p_{t_{n+1}} \textcolor{red}{≈} s_\theta(x_{t_{n+1}},t_{n+1})$ 其中 $s_\theta$代表的是训练好的去噪网络。

那么这样一来整个过程就变成了：

回顾整个过程（直接借鉴上面的流程图），算法比较简单（只不过背后的数学原理蛮复杂），简单描述上面过程就是：对于输入图片通过加噪处理之后得到加噪的图像，损失函数设计就是直接通过计算相邻的两步之间的“距离”最小，对于 $x_{t_{n+1}}$ 我们是已经知道的，但是对于当前时间 $t_n$ 是未知的，因此可以直接通过ODE solver的方式去进行估计，而后再去计算loss并且更新参数。

直接训练模型进行优化

直接训练模型进行优化，其中具体的过程为：

LCM/LCM-Lora

潜在一致性模型（Latent Consistency Model）⁴以及LCM-Lora⁵（LCM的Lora优微调）通过再latent space中使用一致性模型（stable diffusion model通过VAE将图像进行压缩到latent sapce而后通过DF模型训练并且最后再通过VAE decoder输出），在LCM中主要提出两点：
1、Skipping-Step：因为在最开始的CM中计算两个相邻的时间步之间的loss由于时间步过于接近，就会导致loss很小，因此通过跳步解决这个问题，这样loss就会变成：$d(f(x_{t_{n+\textcolor{red}{k}}}, t_{n+\textcolor{red}{k}}), f(x_{t_n}, t_n))$。
2、引入Classifier-free guidance (CFG) 那么整个loss计算就会变成：$d(f(x_{t_{n+\textcolor{red}{k}}}, \textcolor{red}{w}+ \textcolor{red}{c}, t_{n+\textcolor{red}{k}}), f(x_{t_n}, \textcolor{red}{w}+ \textcolor{red}{c}+ t_n))$，公式中c代表文本，对于CFG而言其实就是一个改进的ODE solver（见下面算法流程中的蓝色部分）

对于LCD算法流程，其中蓝色部分为LCM所修改的内容：

对于最后得到的实验结果分析：

• 不同的k对结果的影响

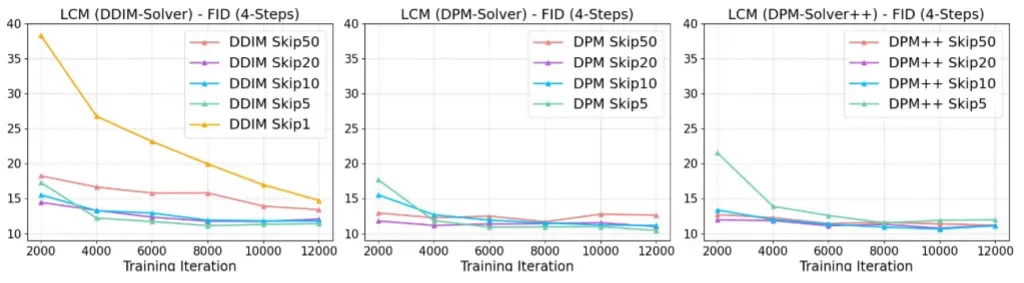
在DPM-solver++和DPM-Solver中基本只需要 2000 步迭代，LCM 4 步采样的 FID 就已经基本收敛了

• 不同的Guidance Scale对结果的影响

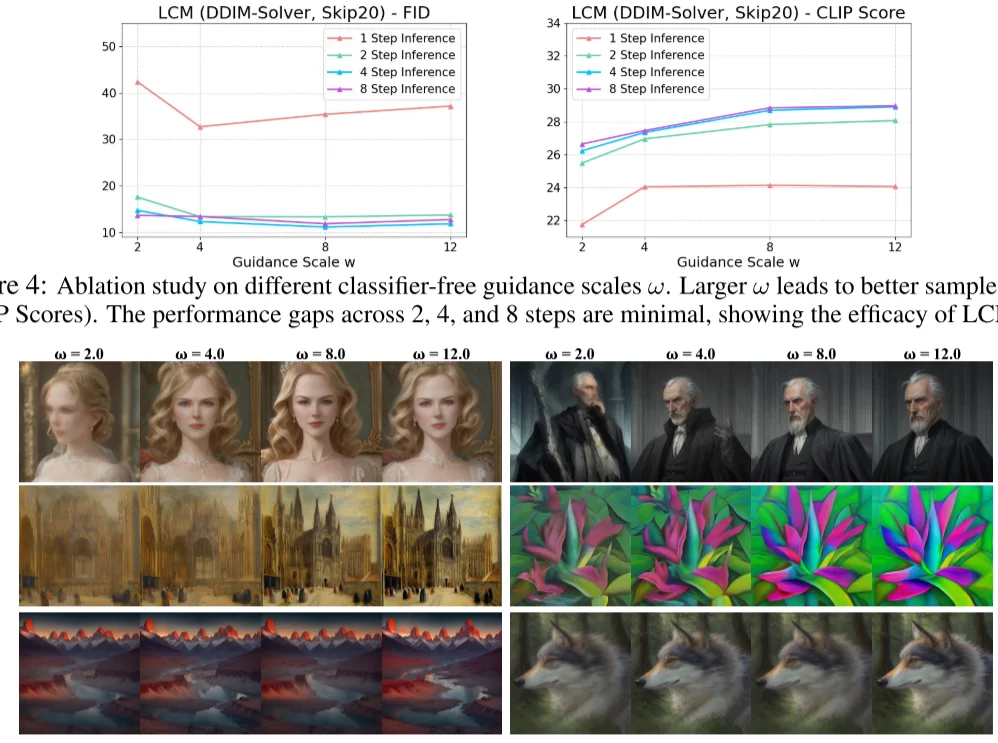
LCM 作者用不同 LCM 的迭代次数与不同 Guidance Scale 做了对比。发现 $w$ 增加有助于提升 CLIP Score，但是损失了 FID 指标（即多样性）的表现。另外，LCM 迭代次数为 2、4、8 时，CLIP Score 和 FID 相差都不大，说明了 LCM 的蒸馏性能确实非常强悍，两步前向的效果可能都足够好了，只是一步前向的结果还差些

TCD⁶

总结

总的来说consistency model作为一种diffusion model生成（区别与DDPM/DDIM）加速操作，在理论上首先将随机生成过程变成“确定”过程，这样一来生成就是确定的，从 $T\rightarrow t_0$ 所有的点都在“一条线”上等式 $f(x_t,t)=f(x_{t^\prime},t^\prime)$ 其中 $t,t^\prime \in [\epsilon,T]$ 成立那么就保证了模型不需要再去不断依靠 $t+1$ 生成内容去推断 $t$时刻内容。而后续的LCM/LCM-Lora/TCD则是基于CM的原理进行改进。

参考