模型训练分析-1：Loss以及Grad Norm分析

在训练模型（Qwen2.5VL-3B）过程中出现奇怪现象：Loss下降但是Grad Norm先下降后上升的情况争对这种情况简单调研分析，首先选择模型以及训练过程中参数如下：Qwen2.5VL-3B、AdamW、cosine（学习率warm up策略）、交叉熵损失函数。而后通过tensorboard记录优化过程loss以及grad_norm，其中记录方式如下：

outputs = model(**batch_data)
loss = outputs.loss
accelerator.backward(loss)
if accelerator.sync_gradients:
    grad_norm = torch.norm(torch.stack(
        [torch.norm(p.grad.detach(), p=2.0) 
         for p in model.parameters() if p.grad is not None])).item()
    accelerator.clip_grad_norm_(model.parameters(), 
                                config.max_grad_norm)
...
if accelerator.sync_gradients:
    progress_bar.update(1)
    global_step += 1
    if accelerator.is_main_process:
        accelerator.log(
            {'Train/Loss': loss.detach().item(), 
             'Train/lr': lr_scheduler.get_last_lr()[0],
             'Train/graid_norm': grad_norm}, 
            step=global_step)

通过上面方式去记录loss等变化情况得到最终图像如下：

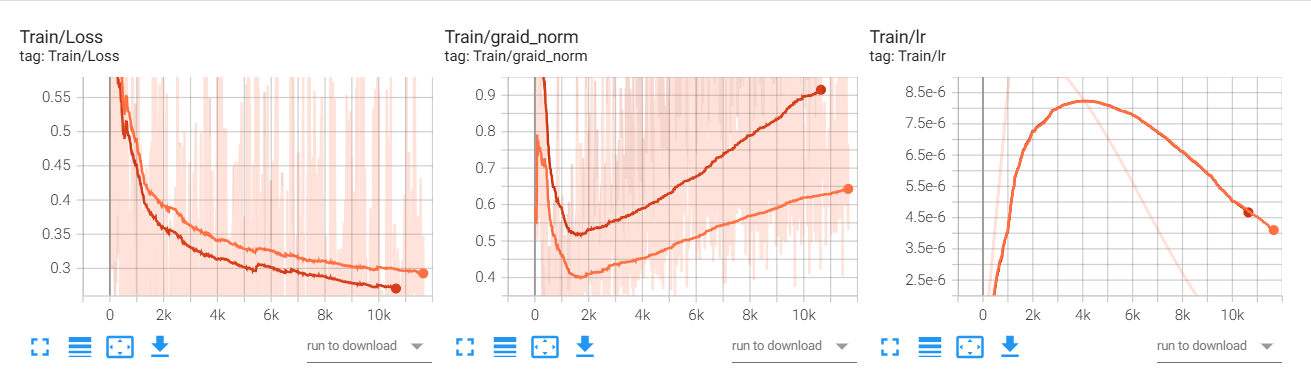
loss以及Grad Norm理论简单分析

首先loss往往直接用来表示模型的拟合效果（loss下降代表拟合效果较好，部分震荡代表数据中部分样本很难较好的进行“拟合”）。Gradient（梯度）一般而言就是对于需要优化函数的导数，而Grad Norm一般就是表示所有参数梯度向量拼接（展平）后形成的超长向量的 L2 范数。在模型训练过程总一般而言主要关注两个指标比较多：1、loss；2、评估指标（ACC等），但是对于Grad Norm这个值相对讨论较少，简单对于Grad Norm过程指标（optimization dynamic 的诊断信号），区别loss它不直接衡量模型好坏，而是反映优化器当前“还能走多远、多快”、训练是否稳定、是否接近某种奇异点等中间状态。
那么理论上而言模型优化过程中应该是loss以及Grad Norm（越往后期模型理论上越接近“最优值”那么梯度理论越小）两个指标都一起下降，但是实际情况可能相反，下面就这种情况简单分析如下：

Grad Norm上升原因分析

在Github-issue¹中给出结论是：梯度范数大致与参数范数成正比（或者至少取决于参数范数）。作者直接给出了梯度与模型参数的变化情况分析：$\Vert \nabla f(\theta) \Vert ≈ \Vert \theta \Vert \cdot \Vert \nabla f(\theta / \Vert \theta \Vert)\Vert$，那么也就意味了如果模型 $\theta / \Vert \theta \Vert$ 大致逐渐收敛但是参数 $\Vert \theta \Vert$在增加就会导致最终的Grad Norm逐渐上升。
在论文中²作者给出解释是：权重衰减与学习率安排相互作用的结果，具体理论分析如下:

这样一来梯度$g$ 与权重 $x_t$ 之间关系就只与学习率 $\gamma$ 和参数 $\lambda$ 之间有关系。因此就可以得到：$\frac{\Vert g_t \Vert}{\Vert x_t \Vert}=\sqrt{\frac{2\lambda}{\gamma_t}}$ 当使用学习率warm up策略时候就会发生下降上升的情况。

模型训练分析-1：Loss以及Grad Norm分析

loss以及Grad Norm理论简单分析

Grad Norm上升原因分析

参考