注意如下内容的描述:1、SDE以及ODE因为不同的调度器可能就是基于不同的方式出发的;2、可以了解一下flow-matching;3、注意LCM模型里面的处理
flow-matching推荐文章
https://diffusionflow.github.io/
SDE以及ODE
在正式介绍之前简短了解一些SDE(随机微分方程)以及ODE(常微分方程),对于ODE一般定义就是:$\frac{dx_t}{dt}=f(x_t,t)$,对于SDE一般定义就是:$dx_t=f(x_t,t)dt+g(x_t,t)dW_t$。两者之间的差异就是SDE会比ODE多一个随机噪声项目,因为多了这个就会导致SDE的轨迹不在唯一每次的求解都是不同的,那么SDE/ODE和扩散模型之间联系在哪?
DDPM、DDIM
对于DDPM1以及DDIM2在之前的博客有过简短介绍这里直接将两个放到一起进行介绍。扩散模型过程为:
\[X_T=\sqrt{\bar{\alpha_T}}x_0+ \sqrt{1- \bar{\alpha_T}}\epsilon\]通过对图片($x_0$)不断添加高斯噪声最后得到 $x_T$而后通过反向去噪又得到新的图片。不过DDPM和DDIM之间存在一个很明显的差异就是:DDPM将加(去)噪视作一个马尔科夫链过程(简单理解为每一步 $t$都要依靠上一步 $t-1$),但是在DDIM过程中就会使用“跳步”来进行

DDPM生成过程:
\[x_{t-1}=\frac{1}{\sqrt{\alpha_t}}\left(x_t-\frac{1- \alpha_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_\theta(x_t,t)\right)+\sigma_tz,\quad z\sim\mathcal{N}(0,I)\]但是对于DDPM存在一个最大的问题就是需要多步(一般选择T=1000)来生成图像,这样一来就会导致生成的速度很慢,因此后续就提出了DDIM其中DDIM生成过程为:
\[x_{t-1}=\sqrt{\alpha_{t-1}}\left(\frac{x_t-\sqrt{1-\alpha_t}\epsilon_\theta(x_t,t)}{\sqrt{\alpha_t}}\right)+\sqrt{1-\alpha_{t-1}-\sigma_t^2}\epsilon_\theta(x_t,t)+\sigma_tz\]重点了解一下在diffusers库中如何处理这两个调度器的,以DDPM(源代码)为例,一般来说使用调度器无疑就是下面几个步骤:
from diffusers import DDPMScheduler
# 直接使用初始化的 调度器
noise_scheduler = DDPMScheduler(num_train_timesteps= config.num_train_timesteps,
beta_start= config.beta_start,
beta_end= config.beta_end,
beta_schedule= 'scaled_linear')
# 或则直接加载其他的模型的调度器
noise_scheduler = DDPMScheduler.from_pretrained("stabilityai/stable-diffusion-xl-base-1.0", cache_dir= config.cache_dir, subfolder="scheduler")
'''
不过值得注意的是在DDIM中会:noise_scheduler.set_timesteps(inference_steps) 来告诉用多少步进行推理()
'''
# 将噪声添加到图片上
noise = torch.randn(image.shape, device= accelerator.device)
noise_image = noise_scheduler.add_noise(image, noise, timesteps)
...
# 将噪声进行剔除
noise = noise_scheduler.step(predicted_noise, t, noise).prev_sample
简短了解一下在DDPMScheduler中设计框架是如何的:
class DDPMScheduler(SchedulerMixin, ConfigMixin):
@register_to_config
def __init__(
self,
num_train_timesteps: int = 1000, # 加噪的步数
beta_start: float = 0.0001, # \beta 起始数值
beta_end: float = 0.02, # \beta 最后数值
beta_schedule: str = "linear", # 线性加噪方式
...)
...
if ...:
...
elif beta_schedule == "linear":
self.betas = torch.linspace(beta_start, beta_end, num_train_timesteps, dtype=torch.float32)
# 1、初始化参数
self.alphas = 1.0 - self.betas
self.alphas_cumprod = torch.cumprod(self.alphas, dim=0)
...
self.timesteps = torch.from_numpy(np.arange(0, num_train_timesteps)[::-1].copy())
def add_noise(
self,
original_samples: torch.Tensor,
noise: torch.Tensor,
timesteps: torch.IntTensor,)
# 2、加噪过程
self.alphas_cumprod = self.alphas_cumprod.to(device=original_samples.device)
alphas_cumprod = self.alphas_cumprod.to(dtype=original_samples.dtype)
timesteps = timesteps.to(original_samples.device)
sqrt_alpha_prod = alphas_cumprod[timesteps] ** 0.5
sqrt_alpha_prod = sqrt_alpha_prod.flatten()
while len(sqrt_alpha_prod.shape) < len(original_samples.shape):
sqrt_alpha_prod = sqrt_alpha_prod.unsqueeze(-1)
sqrt_one_minus_alpha_prod = (1 - alphas_cumprod[timesteps]) ** 0.5
sqrt_one_minus_alpha_prod = sqrt_one_minus_alpha_prod.flatten()
while len(sqrt_one_minus_alpha_prod.shape) < len(original_samples.shape):
sqrt_one_minus_alpha_prod = sqrt_one_minus_alpha_prod.unsqueeze(-1)
noisy_samples = sqrt_alpha_prod * original_samples + sqrt_one_minus_alpha_prod * noise
return noisy_samples
def step(
self,
model_output: torch.Tensor,
timestep: int,
sample: torch.Tensor,
generator=None,
return_dict: bool = True,):
# 3、生成过程
t = timestep
prev_t = self.previous_timestep(t)
# 首先计算 alpha等参数
alpha_prod_t = self.alphas_cumprod[t]
alpha_prod_t_prev = self.alphas_cumprod[prev_t] if prev_t >= 0 else self.one
beta_prod_t = 1 - alpha_prod_t
beta_prod_t_prev = 1 - alpha_prod_t_prev
current_alpha_t = alpha_prod_t / alpha_prod_t_prev
current_beta_t = 1 - current_alpha_t
# 而后计算 预测结果 DDPM有3种计算过程 epsilon sample v_prediction
if self.config.prediction_type == "epsilon":
pred_original_sample = (sample - beta_prod_t ** (0.5) * model_output) / alpha_prod_t ** (0.5)
...
# 裁剪预测值
...
elif self.config.clip_sample:
pred_original_sample = pred_original_sample.clamp(
-self.config.clip_sample_range, self.config.clip_sample_range
)
# important
1、初始化参数(DDPM和DDIM中没什么差异)。首先是根据 beta_schedule来生成在 num_train_timesteps下参数 $\beta$的值(比如说 linear那么在1000步下就会生成(直接通过torch.linspace)从 (1-beta_start)-(1-beta_end) 的1000个数字)而后就是定义好加噪比较重要的几个参数:$\alpha$ 以及迭代次数 $t$,对于self.alphas_cumprod则是直接计算累乘得到的结果。上面过程对应:
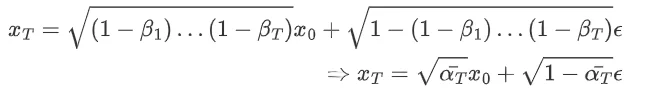
2、加噪过程(DDPM和DDIM中没什么差异)。这个整个过程也比较简单就是直接通过计算:$X_T=\sqrt{\bar{\alpha_T}}x_0+ \sqrt{1- \bar{\alpha_T}}\epsilon$
3、生成过程。输入三个参数分别表示:1、model_output:模型预测得到的噪声数值;2、timestep:时间步;3、sample:就是我们加载后的$x_t$(最开始就是一个纯噪声随着迭代逐渐“清晰”)。生成图像过程中无疑就是直接通过$t$去推导 $t-1$的图像结果,因此在DDPM生成过程中 首先是分别计算 $\alpha_{t}$以及 $\alpha_{t-1}$,不过生成过程有三种。
epsilon:预测噪声 $\epsilon$(将上面加噪公司逆推得到$x_0$)sample:直接用 $x_0$就是模型的输出v_prediction:预测$v$(Stable Diffusion 2.x一般就是这个)
最重要的是后面的 important部分代码,在DDPM中需要计算:
代码中对应:
pred_original_sample_coeff = (alpha_prod_t_prev ** (0.5) * current_beta_t) / beta_prod_t
current_sample_coeff = current_alpha_t ** (0.5) *beta_prod_t_prev / beta_prod_t
pred_prev_sample = pred_original_sample_coeff *pred_original_sample + current_sample_coeff * sample
最后在模型里面会返回两部分内容:1、pred_prev_sample;2、pred_original_sample。对于这两个值分别表示的是:模型认为最终的干净图像(完全无噪声)(pred_original_sample)。采样一步后,预计在第 499 步应该长的样子(pred_prev_sample)。对比在DDIM中的差异,第一个就是时间步处理差异,在DDPM中直接用$t-1$来获取上一步就行,但是在DDIM中需要计算timestep - self.config.num_train_timesteps // self.num_inference_steps这是因为DDIM会使用“跳步”;2、在计算 $x_0$上两者之间不存差异,只是计算上一步在公式上存在差异(DDIM计算公式):
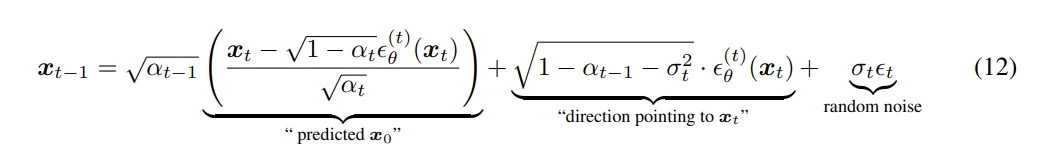
variance = self._get_variance(timestep, prev_timestep)
std_dev_t = eta * variance ** (0.5)
if use_clipped_model_output:
pred_epsilon = (sample - alpha_prod_t ** (0.5) * pred_original_sample) / beta_prod_t ** (0.5)
pred_sample_direction = (1 - alpha_prod_t_prev - std_dev_t**2) ** (0.5) * pred_epsilon
prev_sample = alpha_prod_t_prev ** (0.5) * pred_original_sample + pred_sample_direction
不同调度器生成对比
只是简单对比不同调度器在生成效果上的速度差异(SDXL模型)
不同调度器生成对比,从上面简单比较发现一般来说需要20-30步(建立在不适用LCM模型基础上)才能生成一个效果较好的图像,从测试过程发现基本(20-30步)一张图片消耗时间为0.2s左右(A100-80G以及使用float16)。从上面的测试结果上来看UniPCMultistepScheduler和 DPMSolverMultistepScheduler测试的效果最好(仅仅只从迭代步数上分析),借用ChatGPT对不同生成器的分析如下:
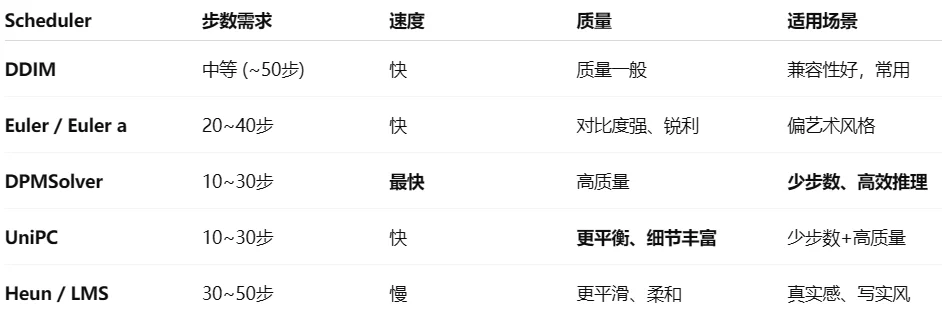
不过如果去仔细看生成图像的细节内容的话(单独对比了Unip、DPM、DDIM从10-50步使用的模型是SDXL并且使用float16)得到测试结果
此过程使用的prompt(直接GPT生成):
validation_prompt = [ # 1. 动态多主体 + 复杂光影 "A fierce dog fighting a cat inside a Victorian living room, ultra realistic fur, dynamic cinematic lighting, motion blur, 8k hyper detail, dramatic shadows, volumetric fog", # 2. 科幻场景 + 光影/反射 "A futuristic cyberpunk city skyline at sunset with flying cars, glowing neon signs, reflective glass skyscrapers, cinematic wide-angle shot, ultra realistic 8k textures, complex lighting, atmospheric haze", # 3. 写实人像 + 材质对比 "A close-up portrait of an elderly woman with deep wrinkles, realistic skin texture, soft diffused lighting, cinematic depth of field, ultra detailed eyes, 8k hyper realism", # 4. 自然风景 + 微距细节 "A crystal-clear mountain lake surrounded by pine trees, sunlight filtering through mist, hyper realistic reflections on water, ultra detailed rocks and moss, 8k cinematic composition", # 5. 奇幻场景 + 复杂材质 "A medieval knight in silver armor standing in a glowing enchanted forest, bioluminescent plants, soft god rays, ultra detailed metallic reflections, cinematic epic fantasy lighting, 8k resolution", # 6. 室内物品 + 精细纹理 "A rustic wooden table with a vintage pocket watch, spilled coffee, handwritten letters, soft morning sunlight, ultra detailed textures, shallow depth of field, 8k macro photography style" ] negative_prompt = "blurry, low quality, distorted, extra limbs, deformed, low contrast, unrealistic lighting, bad anatomy, oversaturated"