pytorch使用-1：pytorch中基础概念

HuangJie 于 2025-07-01 在 武汉🏯 2025-07-01 发布 ⏳ 预计阅读 5 分钟 更新 2025-08-14

1、介绍torch基本知识，比如说：计算图等底层原理
推荐阅读torch官方：https://docs.pytorch.org/docs/stable/notes.html

torch计算图概念

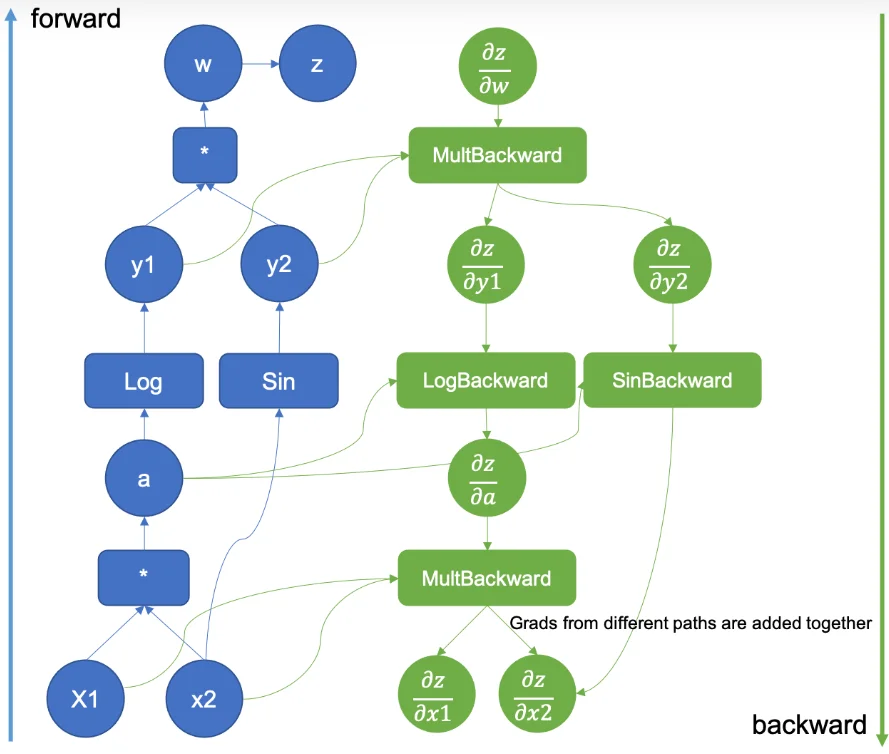
Image

参考上图中给出的例子1，对于（pytorch中的）计算图而言主要起到的作用就是：用来记录张量之间的运算关系。涉及到的几个概念：1、节点（Node）：张量（Tensor）或者运算（Function）。2、边（Edge）：表示数据流和依赖关系，指明一个张量是由哪些运算生成的，或一个运算的输入来源于哪个张量。3、叶子节点（Leaf Tensor）：通常是用户创建的、需要梯度的张量（requires_grad=True）。4、动态计算图：PyTorch 是 动态图框架，计算图会在每次 forward 运行时即时构建，执行完一次计算后，默认图会释放（除非使用retain_graph=True）。当通过调用 .backward() 时，PyTorch 会沿着这个计算图从输出节点反向传播，依次计算每个叶子节点的梯度。比如说对于上面的过程（上面过程中每一个圆圈节点就会对应一个节点，那么反向传播就可以去计算这些节点梯度去对参数进行更新）：$z=w=y_1\times y_2= \log(a) \times \sin(x_2)=\log(x_1\times x_2)+ \sin(x_2)$

import torch

X1 = torch.tensor(2.0, requires_grad=True)
X2 = torch.tensor(3.0, requires_grad=True)

a = X1 * X2                  # a = X1 * X2
y1 = torch.log(a)            # y1 = log(a)
y2 = torch.sin(X2)           # y2 = sin(X2)
w = y1 * y2                  # w = y1 * y2
z = w                        # z = w

a.retain_grad()
y1.retain_grad()
y2.retain_grad()
w.retain_grad()
z.retain_grad()

print("Forward: z =", z.item())
z.backward()
print(f"dz/dz = 1 (输出对自己的梯度永远是1) -> {z.grad.item()}")
print(f"dz/dw = dz/dz * ∂z/∂w = 1 * 1 = {w.grad.item()}")
print(f"dz/dy1 = dz/dw * ∂w/∂y1 = {w.grad.item()} * y2 = {w.grad.item()} * {y2.item()} = {y1.grad.item()}")
print(f"dz/dy2 = dz/dw * ∂w/∂y2 = {w.grad.item()} * y1 = {w.grad.item()} * {y1.item()} = {y2.grad.item()}")
print(f"dz/da  = dz/dy1 * ∂y1/∂a = {y1.grad.item()} * (1/a) = {y1.grad.item()} * (1/{a.item()}) = {a.grad.item()}")
print(f"dz/dX1 = dz/da * ∂a/∂X1 = {a.grad.item()} * X2 = {a.grad.item()} * {X2.item()} = {X1.grad.item()}")
print(f"dz/dX2 = dz/da * ∂a/∂X2 + dz/dy2 * ∂y2/∂X2\n"
      f"       = {a.grad.item()} * X1 + {y2.grad.item()} * cos(X2)\n"
      f"       = {a.grad.item()} * {X1.item()} + {y2.grad.item()} * {torch.cos(X2).item()}\n"
      f"       = {X2.grad.item()}")

输出结果为：

Forward: z = 0.2528530955314636
dz/dz = 1 (输出对自己的梯度永远是1) -> 1.0
dz/dw = dz/dz * ∂z/∂w = 1 * 1 = 1.0
dz/dy1 = dz/dw * ∂w/∂y1 = 1.0 * y2 = 1.0 * 0.14112000167369843 = 0.14112000167369843
dz/dy2 = dz/dw * ∂w/∂y2 = 1.0 * y1 = 1.0 * 1.7917594909667969 = 1.7917594909667969
dz/da  = dz/dy1 * ∂y1/∂a = 0.14112000167369843 * (1/a) = 0.14112000167369843 * (1/6.0) = 0.023520000278949738
dz/dX1 = dz/da * ∂a/∂X1 = 0.023520000278949738 * X2 = 0.023520000278949738 * 3.0 = 0.07056000083684921
dz/dX2 = dz/da * ∂a/∂X2 + dz/dy2 * ∂y2/∂X2
       = 0.023520000278949738 * X1 + 1.7917594909667969 * cos(X2)
       = 0.023520000278949738 * 2.0 + 1.7917594909667969 * -0.9899924993515015
       = -1.7267885208129883

对于计算图就是对于你的输入数据进行了那种计算方式进行记录，后续梯度反向传播时候通过上面计算图（计算图保存了所有中间变量和梯度信息）来计算梯度更新参数，那么进一步了解一下这些概念与显存的分析，运行过程中数据的显存占用主要如下几个部分：1、数据本身显存占用；2、数据中间激活（计算图）显存占用。对于这两部分可以直接通过checkpoint以及改变精度来减小显存占用。结果在后续计算中不再需要梯度，可以直接使用 .detach() 将其从计算图中分离，以减少显存占用。

torch数据形状改变方式

在torch中涉及到数据形状改变函数，总结如下：

方法 功能描述 是否拷贝数据 注意事项
reshape() 返回指定形状的新张量，可能会返回原数据的视图，也可能复制数据 视情况而定 当原张量在内存中不连续时会复制数据
view() 返回与原数据共享内存的新张量，形状可变 否 仅适用于内存连续的张量，否则需先 .contiguous()
unsqueeze() 在指定维度插入一个大小为 1 的维度 否 常用于增加 batch 维度或通道维度
squeeze() 删除大小为 1 的维度 否 默认删除所有为 1 的维度，可指定 dim
expand() 扩展张量的某个维度，不复制数据，使用广播 否 扩展的维度只能是 1，否则报错；共享内存需注意修改风险
expand_as() 将张量扩展为与另一个张量形状相同 否 同 expand()，但形状由另一张量决定
transpose() 交换两个维度位置 否 常用于矩阵转置，返回视图
permute() 按指定顺序重新排列所有维度 否 返回视图，但会改变 strides
contiguous() 返回一个内存连续的张量 是（如必要） 常与 view() 搭配使用
clone() 复制张量数据并返回一个新张量 是 独立内存，与原张量不共享存储
detach() 返回与原数据共享内存但不参与计算图的张量 否 常用于切断梯度计算链条

torch多进程

代码：https://github.com/shangxiaaabb/ProjectCode/blob/main/code/Python/DFDataBuild/instance_pipeline/instance_split.py

model.train()、model.eval()、torch.no_grad()

model.train()：把整个模型设为训练模式；如 Dropout 开启、BatchNorm 用小批量统计并更新滑动均值/方差。不影响是否计算梯度。
model.eval()：把模型设为评估/推理模式；如 Dropout 关闭、BatchNorm 使用已累计的运行统计，不再更新。不影响是否计算梯度。
torch.no_grad()：在其上下文中关闭 autograd 记录，从而不构建计算图、不产生 .grad，省显存、加速前向。不改变模型里层的训练/评估行为

参考

  1. https://pytorch.org/blog/computational-graphs-constructed-in-pytorch/ ↩

Footer Image