从梯度消失到模型过拟合：归一化、Dropout 和梯度裁剪的深度解析

HuangJie 于 2025-02-23 在 changsha 2025-02-23 发布 ⏳ 预计阅读 4 分钟 更新 2025-10-16

为了避免提高模型的泛化能力以及训练过程中避免梯度消失/梯度爆炸现象发生，我们通常会在神经网络中引入一系列“训练稳定性机制”。其中，归一化（Normalization）技术、Dropout 正则化和梯度裁剪（Gradient Clipping）是被广泛采用的三种核心手段：

定义如下计算公式：

\[\mu_i= \frac{1}{m}\sum_{k\in S_i}x_k\] \[\sigma_i= \sqrt{\frac{1}{m}\sum_{k\in S_i}(x_k- \mu_i)^2+\epsilon}\]

4类标准化区别就在于对于参数$S_i$的定义！！！（也就是沿着哪个维度进行归一化处理）
如：对一组图片定义如下变量：$(N,C,H,W)$分别代表：batch、channel、height、width
Bath-norm：$S_i={k_C=i_C}$
Layer-norm：$S_i={k_C=i_N}$
Instance-norm：$S_i={k_C=i_C,K_N=i_N}$
Group-norm：$S_i={k_N=i_N, \lfloor \frac{k_C}{C/G} \rfloor=\lfloor \frac{i_C}{C/G} \rfloor}$
$G$代表组的数量，$C/G$每个组的通道数量

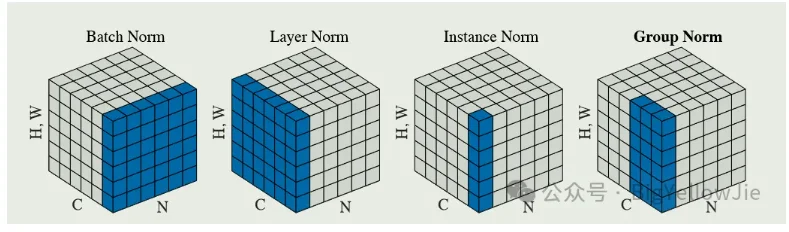
Image

上图都是在image上做的例子

BatchNorm
BN应用于一批数据中的单个特征，通过计算批处理上特征的均值和方差来独立地归一化每个特征。它允许更高的学习率，并降低对网络初始化的敏感性。
这种规范化发生在每个特征通道上，并应用于整个批处理维度，它在大型批处理中最有效，因为统计数据是在批处理中计算的。

LayerNorm
LN计算用于归一化单个数据样本中所有特征的均值和方差。它应用于每一层的输出，独立地规范化每个样本的输入，因此不依赖于批大小。
LN有利于循环神经网络(rnn)以及批处理规模较小或动态的情况。

RMSnorm
From：https://pytorch.org/docs/stable/generated/torch.nn.modules.normalization.RMSNorm.html

$y_i=\frac{x_i}{RMS(x)}*\gamma_i$，其中 $RMS(x)=\sqrt{\epsilon+ \frac{1}{n}\sum_{i=1}^{n}x_i^2}$
和 LayerNorm之间区别就在于没有减均值这一步的操作

InstanceNorm
IN对每个样本的每个通道进行独立的归一化处理
GroupNorm
GN将通道道分成若干组，并计算每组内归一化的均值和方差。这对于通道数量可能很大的卷积神经网络很有用，将它们分成组有助于稳定训练。GN不依赖于批大小，因此适用于小批大小的任务或批大小可以变化的任务。
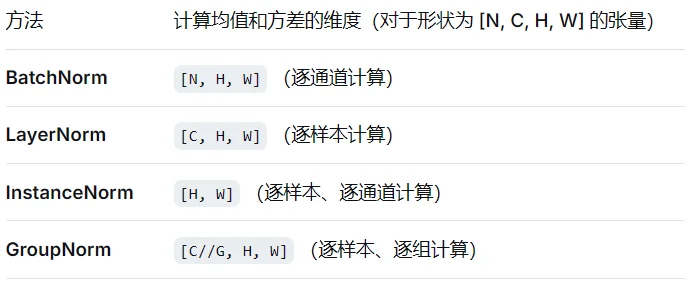
不同归一化对比：

方法 归一化范围 依赖 batch size 应用场景 原因
BatchNorm Mini-batch 的每个维度 是 分类任务，CNN，较大 batch size 1. 通过 mini-batch 的统计信息减少特征偏移，保持分布稳定。
2. 在分类任务中，特征分布的稳定性有助于提升模型收敛速度和最终性能。
LayerNorm 单个样本的所有特征 否 NLP，RNN，Transformer 1. 在 NLP 和序列建模中，训练的样本通常较小，不依赖 batch 统计量的 LayerNorm 更稳定。
2. 对整个样本归一化，使得模型对序列长度或上下文无关。
InstanceNorm 单个样本的每个通道独立 否 风格迁移，生成任务 1. 强调样本内部特征分布的一致性，适合强调局部特征（如风格迁移中的纹理）。
2. 不考虑全局或跨样本的统计信息，能更好保留样本特有的风格特性。
GroupNorm 分组特征 否 小 batch 或单样本 CNN 1. 对小 batch 或单样本任务，避免了 BatchNorm 的统计不稳定问题。
2. 分组归一化平衡了跨通道信息的利用和归一化稳定性，适合卷积特征提取。

From: https://blog.csdn.net/qq_36560894/article/details/115017087

BatchNorm：在同一个特征通道（Channel）内，跨一个批次的 所有样本（N）和空间位置（H, W） 计算均值和方差。对batch size敏感。当batch size很小（比如1或2）时，计算的均值和方差噪声很大，不足以代表整个数据分布，导致效果变差。
LayerNorm：在单个样本内，对所有特征（通常是所有通道C和空间位置H, W）计算均值和方差。与batch size无关，非常适合小批量或在线学习。因为它对单个样本的所有特征进行归一化，非常适合处理变长序列（如自然语言），因为它的计算不依赖于序列长度
InstanceNorm：在单个样本的单个通道内，对所有空间位置计算均值和方差。可以看作是“批大小为1的BatchNorm”，但它是逐样本、逐通道独立进行的
GroupNorm：是LayerNorm和InstanceNorm的折中。将通道（C）分成G个组（Group），然后在单个样本的每个组内，计算所有通道和空间位置的均值和方差。
Image
代码：（pytorch）

import torch
import torch.nn as nn

x = torch.randn(32, 64, 32, 32)
batch_norm = nn.BatchNorm2d(64)
layer_norm = nn.LayerNorm([64, 32, 32])
group_norm = nn.GroupNorm(8, 64) # 对64通道分8组
isins_norm = nn.InstanceNorm2d(64)
rms_norm = nn.RMSNorm([64, 32, 32])

out_batch = batch_norm(x)
out_layer = layer_norm(x)
out_gropu = group_norm(x)
out_insta = isins_norm(x)
out_rms = rms_norm(x)

InstanceNorm2d、GroupNorm、LayerNorm、BatchNorm2d
假设输入形状: N,C,H,W
1、InstanceNorm2d和BatchNorm2d在代码实践上相似都是对C计算
2、LayerNorm对于输入为N,C,H,W（比如说图像）那么选择C,H,W，如果输入为N,Dim1,Dim2（比如说文本）那么对 Dim2计算
3、GroupNorm则是对C分n个组

2、Dropout

在 Dropout 中，每个神经元在训练过程中有一定概率$𝑝$, $p$被随机设置为 0（即被“丢弃”），这种行为可以用如下数学公式描述：
假设某一层神经元的输入表示为一个向量$x=[x_1,… x_n]$该层输出为：$y=[y_1,…,y_n]$，那么Dropout计算过程：首先随机生成掩码向量：$r_i \sim Bernoulli(p),i=1,…,n$（$P(r_i=1)=p, P(r_i=0)=1-p$），对输入进行掩码得到：$\tilde{x}=r \odot x$其中$\odot$代表按元素相乘（其实整个过程也就是随机将神经元乘0）
反向传播过程中：对于被Dropout的神经元其梯度也会被置于0

3、梯度裁剪策略

梯度裁剪（Gradient Clipping）是一种在训练神经网络时常用的技术，它用于防止梯度爆炸问题。梯度爆炸是指在训练过程中，梯度的大小急剧增加，导致权重更新过大，从而使得模型无法收敛或者性能急剧下降的现象。在PyTorch中，可以使用 torch.nn.utils.clip_grad_norm 或 torch.nn.utils.clip_grad_value_ 函数来实现梯度裁剪。

\[g\leftarrow{g}\frac{max_norm}{||g||_{2}}\] 
torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)

所有的模型参数梯度如果整体范数超过1就会被缩放

直接将每一个参数的梯度值限制在指定范围内，超过范围就被“硬截断”。不考虑整体范数，只关注单个数值大小。

torch.nn.utils.clip_grad_value_(model.parameters(), clip_value=0.5)

这样一来模型梯度就会被限制在$[-0.5,0.5]$

Footer Image